想实现个循环缓冲区(CircularBuffer),搜了些资料多数是基于循环队列的实现形式。使用一个变量储存缓冲区中的数据宽度或则空下来一个空间来判定缓冲区是否满了。碰巧间见到剖析Linux内核的循环缓冲队列kfifo的实现,确实非常巧妙。kfifo主要有以下特性:
本文主要以下三个部份:
关于显存屏障的本文不作过多剖析,可以参考WikiMemoryBarrier。另外,本文所涉及的整数都默认为无符号整数,不再做一一说明。
1.2的次幂2.Linux实现kfifo及剖析
Linux内核中kfifo实现方法,主要集中在装入数据的put方式和取数据的get方式。代码如下:
unsigned int __kfifo_put(struct kfifo *fifo, unsigned char *buffer, unsigned int len) { unsigned int l; len = min(len, fifo->size - fifo->in + fifo->out); /* * Ensure that we sample the fifo->out index -before- we * start putting bytes into the kfifo. */ smp_mb(); /* first put the data starting from fifo->in to buffer end */ l = min(len, fifo->size - (fifo->in & (fifo->size - 1))); memcpy(fifo->buffer + (fifo->in & (fifo->size - 1)), buffer, l); /* then put the rest (if any) at the beginning of the buffer */ memcpy(fifo->buffer, buffer + l, len - l); /* * Ensure that we add the bytes to the kfifo -before- * we update the fifo->in index. */ smp_wmb(); fifo->in += len; return len; } unsigned int __kfifo_get(struct kfifo *fifo,unsigned char *buffer, unsigned int len) { unsigned int l; len = min(len, fifo->in - fifo->out); /* * Ensure that we sample the fifo->in index -before- we * start removing bytes from the kfifo. */ smp_rmb(); /* first get the data from fifo->out until the end of the buffer */ l = min(len, fifo->size - (fifo->out & (fifo->size - 1))); memcpy(buffer, fifo->buffer + (fifo->out & (fifo->size - 1)), l); /* then get the rest (if any) from the beginning of the buffer */ memcpy(buffer + l, fifo->buffer, len - l); /* * Ensure that we remove the bytes from the kfifo -before- * we update the fifo->out index. */ smp_mb(); fifo->out += len; return len; } put返回实际保存到缓冲区中的数据宽度,get返回的是实际取到的数据宽度。在里面代码中,须要注意到在写入、取出时侯的两次min运算。关于kfifo的剖析,已有好多资料了,也可参考眉宇传情之匠心独运的kfifo。

Linux内核实现的kfifo的有以下特性:
优点:
实现单消费者和单生产者的无锁并发访问。多消费者和多生产者的时侯还是须要加锁的。使用与运算in&(size-1)取代模运算
在更新in或则out的值时不做模运算,而是让其手动溢出。这应当是kfifo实现最流弊的地方了linux漏洞扫描,借助溢出后的值参与运算模仿linux,而且还能保证结果的正确。溢出运算保证了以下几点:
3.模仿kfifo实现的循环缓冲
主要是模仿其无符号溢出的运算方式,并没有借助显存屏障实现单生产者和单消费者的无锁并发访问。初始化及输入输出的代码如下:
struct kfifo{
uint8_t *buffer;
uint32_t in; // 输入指针
uint32_t out; // 输出指针
uint32_t size; // 缓冲区大小,必须为2的次幂
kfifo(uint32_t _size)
{
if (!is_power_of_2(_size)) _size = roundup_power_of_2(_size); buffer = new uint8_t[_size]; in = 0; out = 0; size = _size; } // 返回实际写入缓冲区中的数据 uint32_t put(const uint8_t *data, uint32_t len) { // 当前缓冲区空闲空间 len = min(len,size - in + out); // 当前in位置到buffer末尾的长度 auto l = min(len, size - (in & (size - 1))); // 首先复制数据到[in,buffer的末尾] memcpy(buffer + (in & (size - 1)), data, l); // 复制剩余的数据(如果有)到[buffer的起始位置,...] memcpy(buffer, data + l, len - l); in += len; // 直接加,不作模运算。当溢出时,从buffer的开始位置重新开始 return len; } // 返回实际读取的数据长度 uint32_t get(uint8_t *data, uint32_t len) { // 缓冲区中的数据长度 len = min(len, in - out); // 首先从[out,buffer end]读取数据 auto l = min(len, size - (out & (size - 1))); memcpy(data, buffer + (out & (size - 1)), l); // 从[buffer start,...]读取数据 memcpy(data + l, buffer, len - l); out += len; // 直接加,不错模运算。溢出后,从buffer的起始位置重新开始 return len; }在初始化缓冲空间的时侯要验证size是否为2的次幂,倘若不是则向下取整为2的次幂。下边注重剖析下在装入取出数据时对表针in和out的处理,以及在溢出后如何才能保证in-out一直为缓冲区中的已有的数据宽度。

put和get方式解读
在向缓冲区中put数据的时侯,须要两个参数:要put的数据表针data和期望才能put的数据宽度len,返回值是实际储存到缓冲区中的数据宽度(当缓冲区中空间不足时该值大于len)。下边详尽的解释下put中每位句子的作用。
由于是循环缓冲区LINUX 删除目录,所以其空闲空间有两部份:从in到缓冲空间的末尾->[in,bufferend]和缓冲空间的起始位置到out->[bufferstart,out]。
get和put很类似,首先判定是否有足够的数据取出;在取数据时首先从out取到buffer的末尾,倘若不够则从buffer的开始位置取;最后更新out时也是不做模运算,让其溢出。看参看前面put的句子解释模仿linux,这儿就不再多说。
无符号溢出运算
kfifo之所以如次的简约,很大一部份要归功于其in和out的溢出运算。这儿就解释下在溢出的情况下,怎样保证in-out一直为缓冲区中的数据宽度。首先来看图:
以上图片引用自linux内核数据结构之kfifo,其对kfifo的剖析也很详尽。
前三种情况下从图中可以很清晰的看出in-out为缓冲区中的已有的数据宽度,并且最后一种发觉in挪到了out的后面,这时侯in-out不是应当为负的么,如何能是数据宽度?这正是kfifo的高明之处,in和out都是无符号整数,这么在in<out时in-out就是正数,把这个正数当成无符号来看时,其值依然是缓冲区中的数据宽度。这和in累加到溢出的情况基本一致,这儿置于一起说。
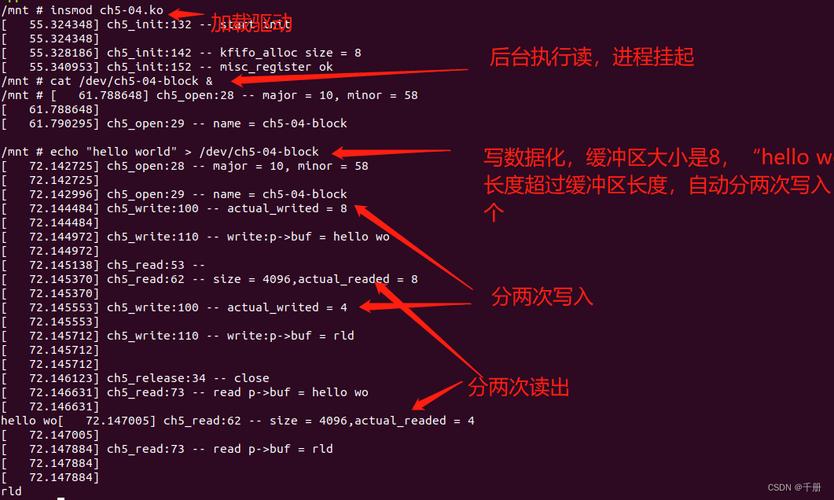
这儿使用8位无符号整数来保存in和out,便捷溢出。这儿假定out=100,in=255,size=256,如右图
/*
--------------------------------------
| | | |
--------------------------------------
out = 100 in = 250 这时缓冲区中已有的数据为:in - out = 150,空闲空间为:size - (in - out) = 106 向缓冲区中put10个数据后 -------------------------------------- | | | | -------------------------------------- in out 这时候 in + 10 = 260 溢出变为in = 4;这是 in - out = 4 - 100 = -96,仍然溢出-96十六进制为`0xA0`,将其直接转换为有符号数`0xA0 = 160`,在没put之前的数据为150,put10个后,缓冲区中的数据刚好为160,刚好为溢出计算结果。 */进行上述运算的前提是,size必须为2的次幂。如果size=257,则上述的运行就不会成功。
测试实例
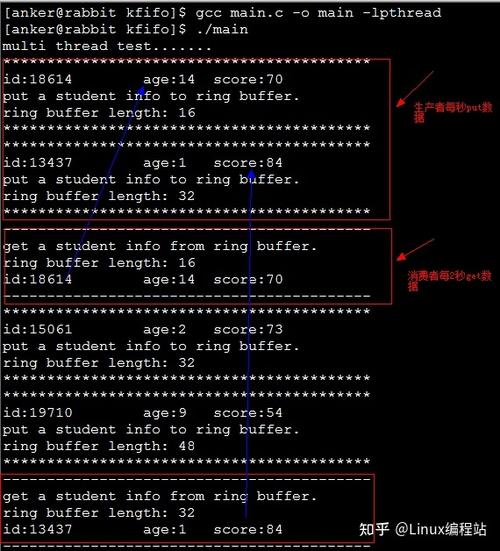
里面描述都是基于运算推论的,下边据结合本文中的代码进行下验证。
测试代码如下:设置空间大小为128,in和out为8位无符号整数
int main()
{
uint8_t output[512] = { 0 }; uint8_t data[256] = { 0 }; for (int i = 0; i < 256; i++) data[i] = i; kfifo fifo(128); fifo.put(data, 100); fifo.get(output, 50); fifo.put(data, 30); auto c = fifo.put(data + 10, 92); cout << "Empty:" << fifo.isEmpty() << endl; cout << "Left Space:" << fifo.left() << endl; cout << "Length:" << fifo.length() << endl; uint8_t a = fifo.size - fifo.in + fifo.out; uint8_t b = fifo.in - fifo.out; cout << "=======================================" << endl; fifo.get(output, 128); cout << "Empty:" << fifo.isEmpty() << endl; cout << "Left Space:" << fifo.left() << endl; cout << "Length:" << fifo.length() << endl; cout << "======================================" << endl; fifo.put(output, 100); cout << "Empty:" << fifo.isEmpty() << endl; auto d = static_cast<uint8_t>(fifo.left()); auto e = static_cast<uint8_t>(fifo.length()); printf("Left Space:%dn", d); printf("Length:%dn", e); getchar(); return 0; }执行结果: